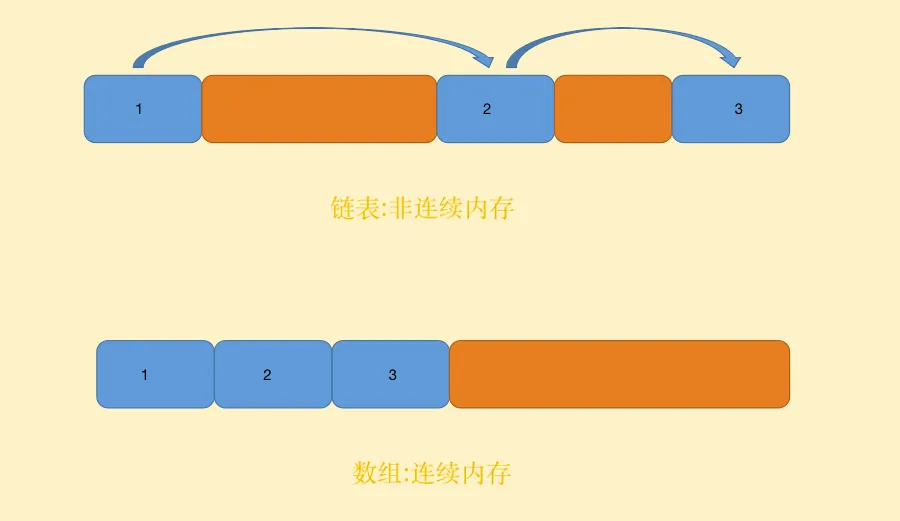
哈希表
哈希表是根据关键码的值而直接进行访问的数据结构。
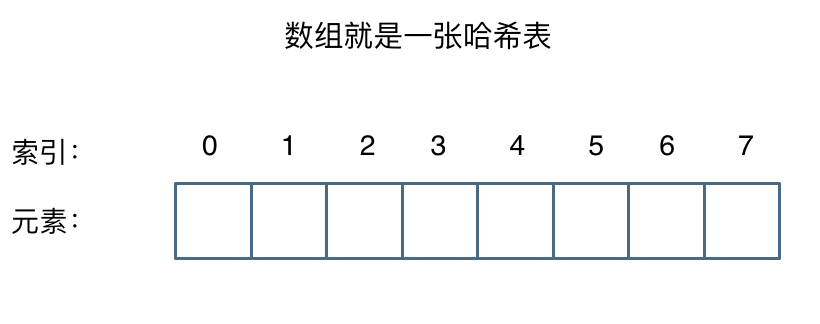
那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断一个元素是否出现集合里。
哈希函数
通过hashCode把名字转化为数值,一般hashcode是通过特定编码方式,可以将其他数据格式转化为不同的数值,这样就把学生名字映射为哈希表上的索引数字了。
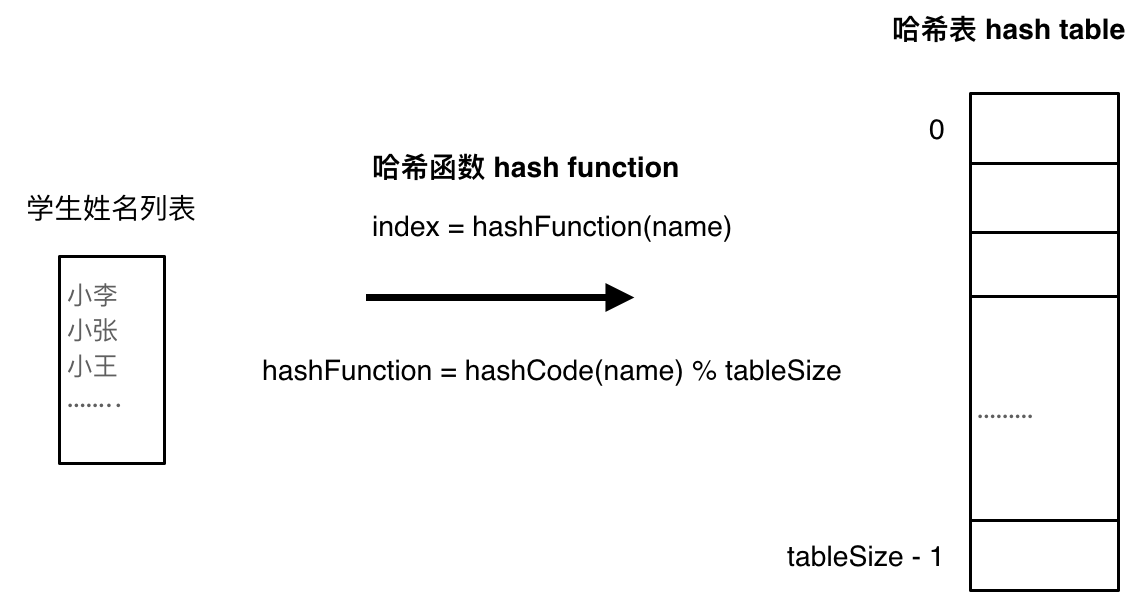
如果hashCode得到的数值大于 哈希表的大小了,也就是大于tableSize了,怎么办呢?
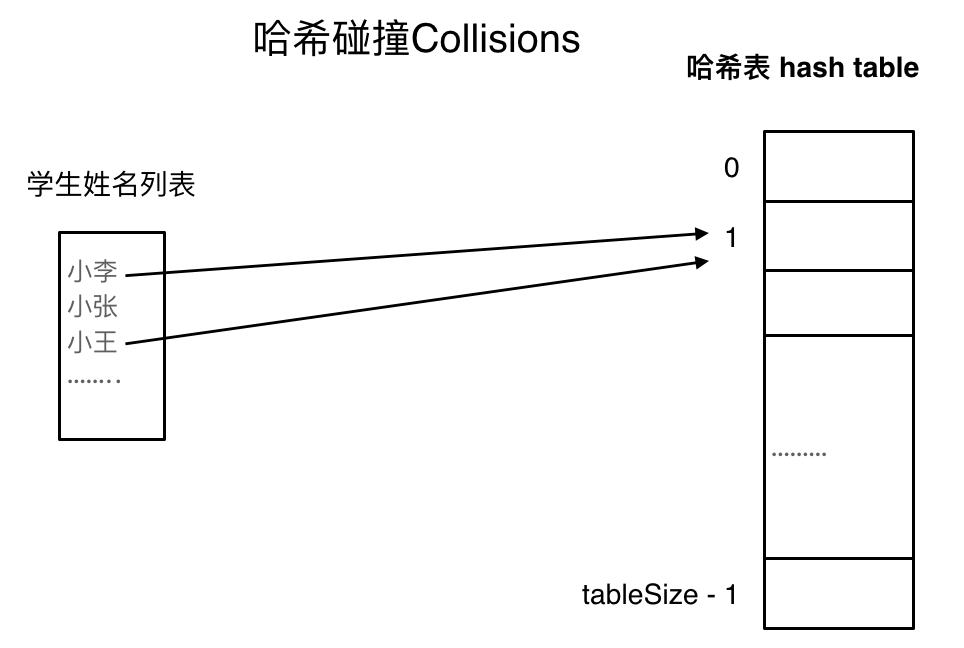
一般哈希碰撞有两种解决方法, 拉链法和线性探测法
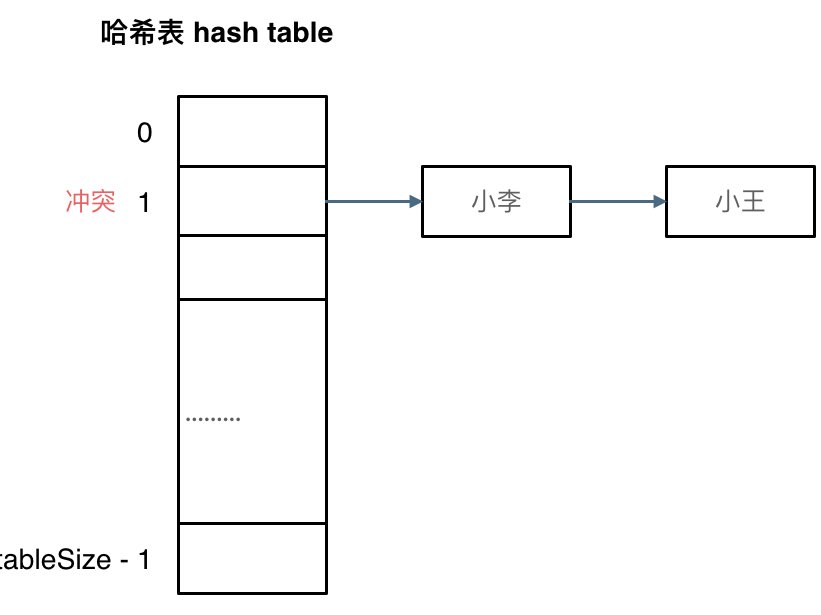
(数据规模是dataSize, 哈希表的大小为tableSize)
其实拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
线性探测法
使用线性探测法,一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。
例如冲突的位置,放了小李,那么就向下找一个空位放置小王的信息。所以要求tableSize一定要大于dataSize ,要不然哈希表上就没有空置的位置来存放 冲突的数据了。如图所示:
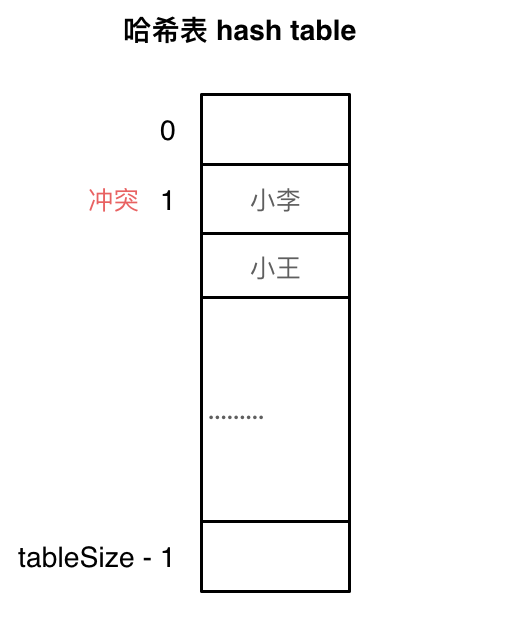
常见的三种哈希结构
当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。
- 数组
- set (集合)
- map(映射)
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。
但是哈希法也是牺牲了空间换取了时间,因为我们要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。
有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例 1: 输入: s = “anagram”, t = “nagaram” 输出: true
示例 2: 输入: s = “rat”, t = “car” 输出: false
说明: 你可以假设字符串只包含小写字母
需要定义一个多大的数组呢,定一个数组叫做record,大小为26 就可以了,初始化为0,因为字符a到字符z的ASCII也是26个连续的数值。
为了方便举例,判断一下字符串s= “aee”, t = “eae”。
操作动画如下:

定义一个数组叫做record用来上记录字符串s里字符出现的次数。
需要把字符映射到数组也就是哈希表的索引下标上,因为字符a到字符z的ASCII是26个连续的数值,所以字符a映射为下标0,相应的字符z映射为下标25。
再遍历 字符串s的时候,只需要将 s[i] - ‘a’ 所在的元素做+1 操作即可,并不需要记住字符a的ASCII,只要求出一个相对数值就可以了。 这样就将字符串s中字符出现的次数,统计出来了。
那看一下如何检查字符串t中是否出现了这些字符,同样在遍历字符串t的时候,对t中出现的字符映射哈希表索引上的数值再做-1的操作。
那么最后检查一下,record数组如果有的元素不为零0,说明字符串s和t一定是谁多了字符或者谁少了字符,return false。
最后如果record数组所有元素都为零0,说明字符串s和t是字母异位词,return true。
class Solution {
public boolean isAnagram(String s, String t) {
int[] record = new int[26];
for (char c : s.toCharArray()) {
record[c - 'a'] += 1;
}
for (char c : t.toCharArray()) {
record[c - 'a'] -= 1;
}
for (int i : record) {
if (i != 0) {
return false;
}
}
return true;
}
}
两个数组的交集
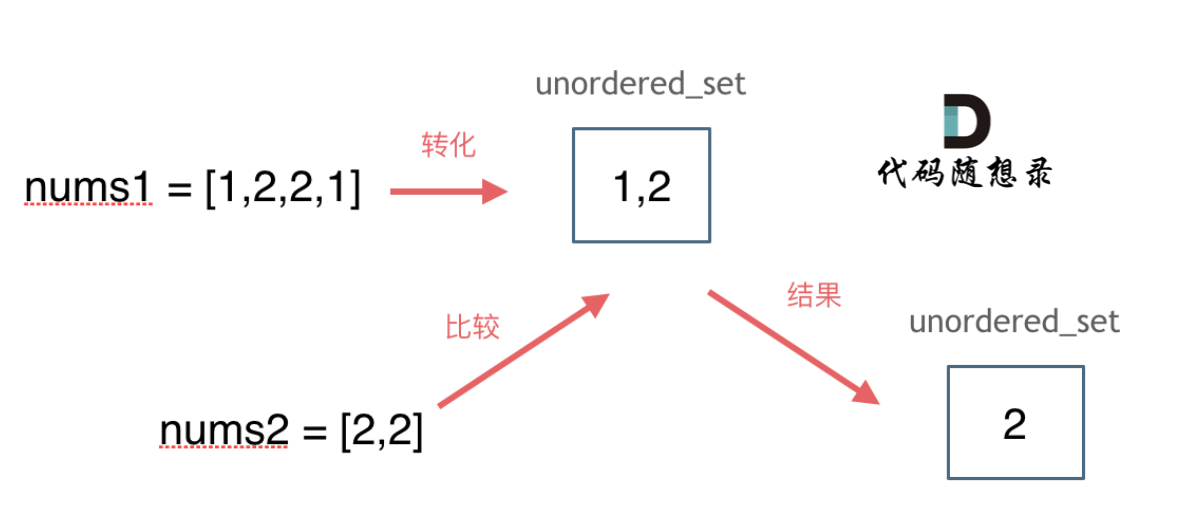
题意:给定两个数组,编写一个函数来计算它们的交集。

说明: 输出结果中的每个元素一定是唯一的。 我们可以不考虑输出结果的顺序
思路
import java.util.HashSet;
import java.util.Set;
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
if (nums1 == null || nums1.length == 0 || nums2 == null || nums2.length == 0) {
return new int[0];
}//泛型写后面会默认set1为Object类型
Set<Integer> set1 = new HashSet<>();
Set<Integer> resSet = new HashSet<>();
//遍历数组1
for (int i : nums1) {
set1.add(i);
}
//遍历数组2的过程中判断哈希表中是否存在该元素
for (int i : nums2) {
if (set1.contains(i)) {
resSet.add(i);
}
}
//将结果几何转为数组
return resSet.stream().mapToInt(x -> x).toArray();
}
}
快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 True ;不是,则返回 False 。
示例:
输入:19
输出:true
解释:
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法了。
所以这道题目使用哈希法,来判断这个sum是否重复出现,如果重复了就是return false, 否则一直找到sum为1为止。
class Solution {
public boolean isHappy(int n) {
HashSet set=new HashSet<Integer>();
while(true){
int sum=getsum(n);
if(sum==1){
return true;
}
if(sum!=1 && !set.contains(n)){
set.add(n);
}
if(sum!=1 && set.contains(n)){
return false;
}
}
}
int getsum(int n){
int sum=0;
while(n>0){
sum=(n%10)*(n%10);
n=n/10;
}
return sum;
}
}
两数之和
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
什么时候使用哈希法,当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
我们不仅要知道元素有没有遍历过,还有知道这个元素对应的下标,需要使用 key value结构来存放,key来存元素,value来存下标,那么使用map正合适。
使用数组和set来做哈希法的局限。
- 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
- set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下标位置,因为要返回x 和 y的下标。所以set 也不能用。
map中key和value分别表示什么
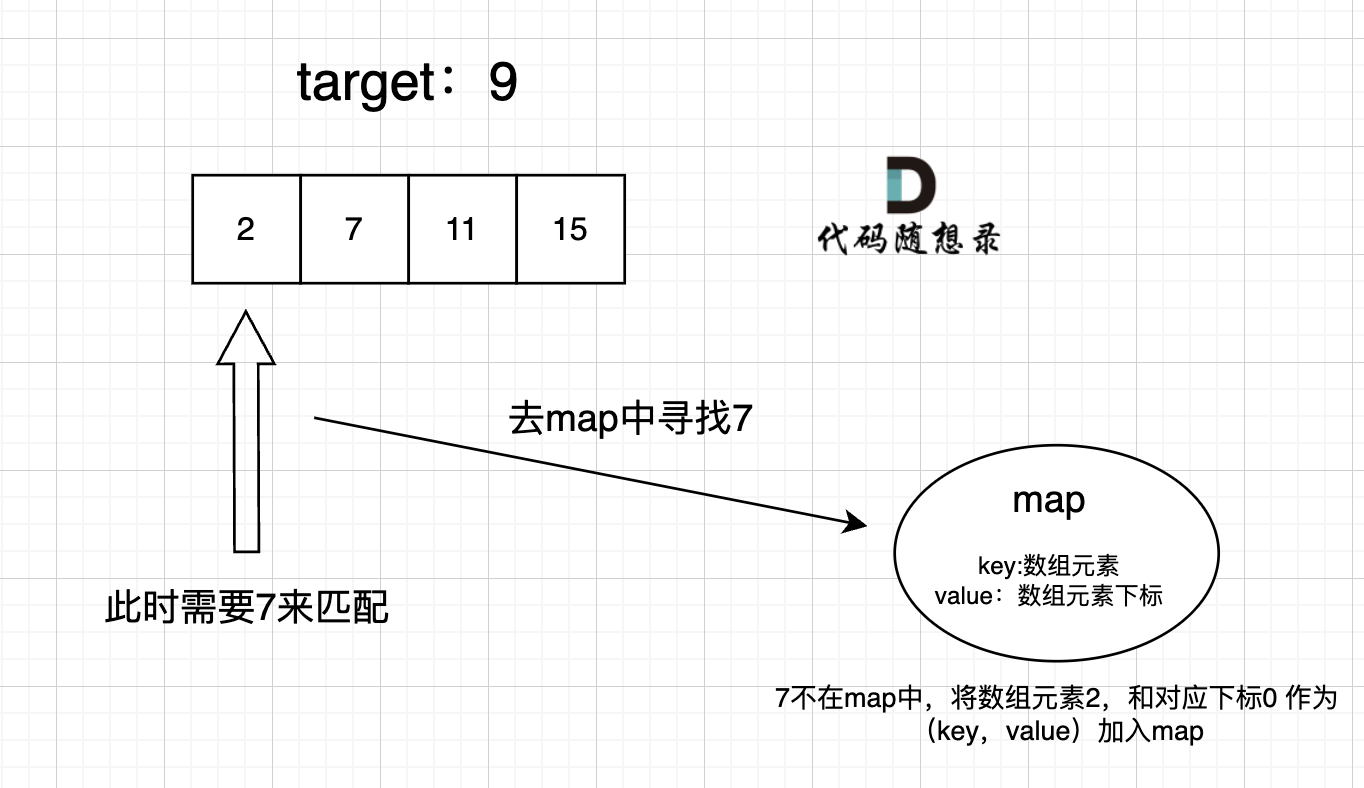
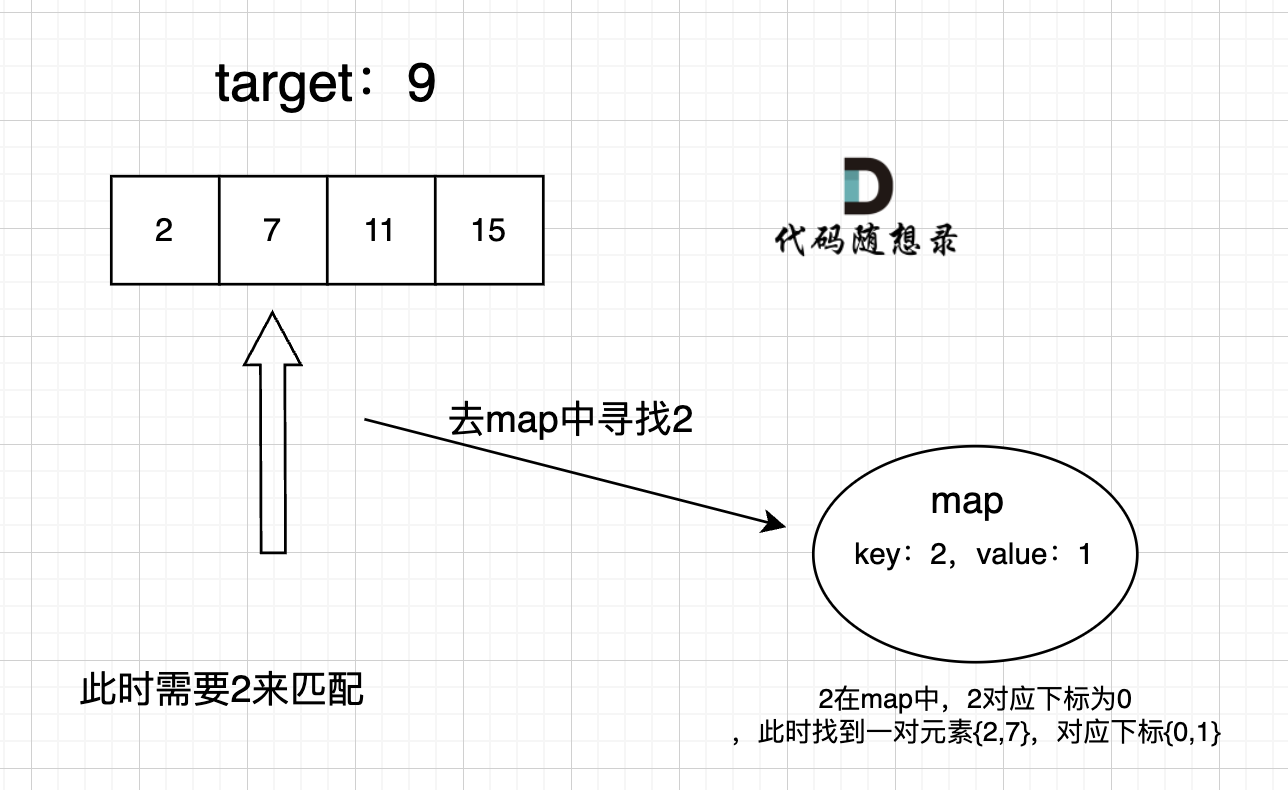
map目的用来存放我们访问过的元素,因为遍历数组的时候,需要记录我们之前遍历过哪些元素和对应的下表,这样才能找到与当前元素相匹配的(也就是相加等于target)
在遍历数组的时候,只需要向map去查询是否有和目前遍历元素比配的数值,如果有,就找到的匹配对,如果没有,就把目前遍历的元素放进map中,因为map存放的就是我们访问过的元素。
//暴力算法
class Solution {
public int[] twoSum(int[] nums, int target) {
int[] a=new int[2];
for(int i=0;i<nums.length;i++){
for(int j=i+1;j<nums.length;j++){
if(nums[i]+nums[j]==target){
a[0]=i;
a[1]=j;
break;
}
}
}
return a;
}
}
public int[] twoSum(int[] nums, int target) {//哈希算法
int[] res = new int[2];
if(nums == null || nums.length == 0){
return res;
}
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < nums.length; i++){
int temp = target - nums[i];
if(map.containsKey(temp)){
res[1] = i;
res[0] = map.get(temp);
}
map.put(nums[i], i);
}
return res;
}
四数相加II
给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ,使得 A[i] + B[j] + C[k] + D[l] = 0。
为了使问题简单化,所有的 A, B, C, D 具有相同的长度 N,且 0 ≤ N ≤ 500 。所有整数的范围在 -2^28 到 2^28 - 1 之间,最终结果不会超过 2^31 - 1 。
例如:
输入:
- A = [ 1, 2]
- B = [-2,-1]
- C = [-1, 2]
- D = [ 0, 2]
输出:
2
解释:
两个元组如下:
- (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
- (1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0
本题是使用哈希法的经典题目,而三数之和0018.四数之和 并不合适使用哈希法,因为三数之和和四数之和这两道题目使用哈希法在不超时的情况下做到对结果去重是很困难的,很有多细节需要处理。
而这道题目是四个独立的数组,只要找到A[i] + B[j] + C[k] + D[l] = 0就可以,不用考虑有重复的四个元素相加等于0的情况,所以相对于题目18. 四数之和,题目15.三数之和,还是简单了不少!
本题解题步骤:
- 首先定义 一个unordered_map,key放a和b两数之和,value 放a和b两数之和出现的次数。
- 遍历大A和大B数组,统计两个数组元素之和,和出现的次数,放到map中。
- 定义int变量count,用来统计 a+b+c+d = 0 出现的次数。
- 在遍历大C和大D数组,找到如果 0-(c+d) 在map中出现过的话,就用count把map中key对应的value也就是出现次数统计出来。
- 最后返回统计值 count 就可以了
class Solution {
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
Map<Integer, Integer> map = new HashMap<>();
int temp;
int res = 0;
//统计两个数组中的元素之和,同时统计出现的次数,放入map
for (int i : nums1) {
for (int j : nums2) {
temp = i + j;
if (map.containsKey(temp)) {
map.put(temp, map.get(temp) + 1);
} else {
map.put(temp, 1);
}
}
}
//统计剩余的两个元素的和,在map中找是否存在相加为0的情况,同时记录次数
for (int i : nums3) {
for (int j : nums4) {
temp = i + j;
if (map.containsKey(0 - temp)) {
res += map.get(0 - temp);
}
}
}
return res;
}
}
赎金信
给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串,判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。如果可以构成,返回 true ;否则返回 false。
(题目说明:为了不暴露赎金信字迹,要从杂志上搜索各个需要的字母,组成单词来表达意思。杂志字符串中的每个字符只能在赎金信字符串中使用一次。)
注意:
你可以假设两个字符串均只含有小写字母。
canConstruct(“a”, “b”) -> false
canConstruct(“aa”, “ab”) -> false
canConstruct(“aa”, “aab”) -> true
哈希解法
因为题目所只有小写字母,那可以采用空间换取时间的哈希策略, 用一个长度为26的数组还记录magazine里字母出现的次数。
然后再用ransomNote去验证这个数组是否包含了ransomNote所需要的所有字母。
依然是数组在哈希法中的应用。
一些同学可能想,用数组干啥,都用map完事了,其实在本题的情况下,使用map的空间消耗要比数组大一些的,因为map要维护红黑树或者哈希表,而且还要做哈希函数,是费时的!数据量大的话就能体现出来差别了。 所以数组更加简单直接有效!
class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
// 定义一个哈希映射数组
int[] record = new int[26];
// 遍历
for(char c : magazine.toCharArray()){
record[c - 'a'] += 1;
}
for(char c : ransomNote.toCharArray()){
record[c - 'a'] -= 1;
}
// 如果数组中存在负数,说明ransomNote字符串总存在magazine中没有的字符
for(int i : record){
if(i < 0){
return false;
}
}
return true;
}
}
三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意: 答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为: [ [-1, 0, 1], [-1, -1, 2] ]
双指针,其实这道题目使用哈希法并不十分合适,因为在去重的操作中有很多细节需要注意
双指针法,这道题目使用双指针法 要比哈希法高效一些,那么来讲解一下具体实现的思路。
动画效果如下:

拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
时间复杂度:O(n^2)。
去重逻辑的思考
a的去重,但这里有一个问题,是判断 nums[i] 与 nums[i + 1]是否相同,还是判断 nums[i] 与 nums[i-1] 是否相同。
都是和 nums[i]进行比较,是比较它的前一个,还是比较他的后一个。
如果我们的写法是 这样:
if (nums[i] == nums[i + 1]) { // 去重操作
continue;
}
那就我们就把 三元组中出现重复元素的情况直接pass掉了。 例如{-1, -1 ,2} 这组数据,当遍历到第一个-1 的时候,判断 下一个也是-1,那这组数据就pass了。
我们要做的是 不能有重复的三元组,但三元组内的元素是可以重复的!所以这里是有两个重复的维度。
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
这么写就是当前使用 nums[i],我们判断前一位是不是一样的元素,在看 {-1, -1 ,2} 这组数据,当遍历到 第一个 -1 的时候,只要前一位没有-1,那么 {-1, -1 ,2} 这组数据一样可以收录到 结果集里。
b与c的去重
去重的逻辑多加了 对right 和left 的去重:
while (right > left) {
if (nums[i] + nums[left] + nums[right] > 0) {
right--;
// 去重 right
while (left < right && nums[right] == nums[right + 1]) right--;
} else if (nums[i] + nums[left] + nums[right] < 0) {
left++;
// 去重 left
while (left < right && nums[left] == nums[left - 1]) left++;
} else {
}
}
但细想一下,这种去重其实对提升程序运行效率是没有帮助的。
拿right去重为例,即使不加这个去重逻辑,依然根据 while (right > left) 和 if (nums[i] + nums[left] + nums[right] > 0) 去完成right– 的操作。
多加了 while (left < right && nums[right] == nums[right + 1]) right--; 这一行代码,其实就是把 需要执行的逻辑提前执行了,但并没有减少 判断的逻辑。
最直白的思考过程,就是right还是一个数一个数的减下去的,所以在哪里减的都是一样的。
所以这种去重 是可以不加的。 仅仅是 把去重的逻辑提前了而已。
思考题
既然三数之和可以使用双指针法,我们之前讲过的两数之和 ,可不可以使用双指针法呢?
两数之和 就不能使用双指针法,要求返回的是索引下标, 而双指针法一定要排序,一旦排序之后原数组的索引就被改变了。
如果两数之和要求返回的是数值的话,就可以使用双指针法了。
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0) {
return result;
}
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.length - 1;
while (right > left) {
int sum = nums[i] + nums[left] + nums[right];
if (sum > 0) {
right--;
} else if (sum < 0) {
left++;
} else {
result.add(Arrays.asList(nums[i], nums[left], nums[right]));
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
right--;
left++;
}
}
}
return result;
}
}
四数之和
题意:给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:
答案中不可以包含重复的四元组。
示例: 给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。 满足要求的四元组集合为: [ [-1, 0, 0, 1], [-2, -1, 1, 2], [-2, 0, 0, 2] ]
四数之和,和三数之和 是一个思路,都是使用双指针法, 基本解法就是在三数之和 的基础上再套一层for循环。
但是有一些细节需要注意,例如: 不要判断nums[k] > target 就返回了,三数之和 可以通过 nums[i] > 0 就返回了,因为 0 已经是确定的数了,四数之和这道题目 target是任意值。比如:数组是[-4, -3, -2, -1],target是-10,不能因为-4 > -10而跳过。但是我们依旧可以去做剪枝,逻辑变成nums[i] > target && (nums[i] >=0 || target >= 0)就可以了。
三数之和 的双指针解法是一层for循环num[i]为确定值,然后循环内有left和right下标作为双指针,找到nums[i] + nums[left] + nums[right] == 0。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值,依然是循环内有left和right下标作为双指针,找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况,三数之和的时间复杂度是O(n^2),四数之和的时间复杂度是O(n^3) 。
那么一样的道理,五数之和、六数之和等等都采用这种解法。
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
// nums[i] > target 直接返回, 剪枝操作
if (nums[i] > 0 && nums[i] > target) {
return result;
}
if (i > 0 && nums[i - 1] == nums[i]) {
continue;
}
for (int j = i + 1; j < nums.length; j++) {
if (j > i + 1 && nums[j - 1] == nums[j]) {
continue;
}
int left = j + 1;
int right = nums.length - 1;
while (right > left) {
long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];
if (sum > target) {
right--;
} else if (sum < target) {
left++;
} else {
result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
left++;
right--;
}
}
}
}
return result;
}
}
一般来说哈希表都是用来快速判断一个元素是否出现集合里。
对于哈希表,要知道哈希函数和哈希碰撞在哈希表中的作用.
哈希函数是把传入的key映射到符号表的索引上。
哈希碰撞处理有多个key映射到相同索引上时的情景,处理碰撞的普遍方式是拉链法和线性探测法。
接下来是常见的三种哈希结构:
- 数组
- set(集合)
- map(映射)
set作为哈希表
在 两个数组的交集 中我们给出了什么时候用数组就不行了,需要用set。
这道题目没有限制数值的大小,就无法使用数组来做哈希表了。
主要因为如下两点:
- 数组的大小是有限的,受到系统栈空间(不是数据结构的栈)的限制。
- 如果数组空间够大,但哈希值比较少、特别分散、跨度非常大,使用数组就造成空间的极大浪费。
所以此时一样的做映射的话,就可以使用set了。
map作为哈希表
使用数组和set来做哈希法的局限。
- 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
- set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下标位置,因为要返回x 和 y的下标。所以set 也不能用。
map是一种<key, value>的结构,本题可以用key保存数值,用value在保存数值所在的下标。所以使用map最为合适。
字符串
反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1:
输入:[“h”,”e”,”l”,”l”,”o”]
输出:[“o”,”l”,”l”,”e”,”h”]
示例 2:
输入:[“H”,”a”,”n”,”n”,”a”,”h”]
输出:[“h”,”a”,”n”,”n”,”a”,”H”]
对于字符串,我们定义两个指针(也可以说是索引下标),一个从字符串前面,一个从字符串后面,两个指针同时向中间移动,并交换元素。
以字符串hello为例,过程如下:

一种就是常见的交换数值:
int tmp = s[i];
s[i] = s[j];
s[j] = tmp;
一种就是通过位运算:
s[i] ^= s[j];
s[j] ^= s[i];
s[i] ^= s[j];
class Solution {
public void reverseString(char[] s) {
for(int i=0,j=s.length-1;i<s.length/2;i++,j--){
char temp=s[i];
s[i]=s[j];
s[j]=temp;
}
}
}
反转字符串II
给定一个字符串 s 和一个整数 k,你需要对从字符串开头算起的每隔 2k 个字符的前 k 个字符进行反转。
如果剩余字符少于 k 个,则将剩余字符全部反转。
如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
示例:
输入: s = “abcdefg”, k = 2
输出: “bacdfeg”
在遍历字符串的过程中,只要让 i += (2 * k),i 每次移动 2 * k 就可以了,然后判断是否需要有反转的区间。
因为要找的也就是每2 * k 区间的起点,这样写,程序会高效很多。
//解法一
class Solution {
public String reverseStr(String s, int k) {
StringBuffer res = new StringBuffer();
int length = s.length();
int start = 0;
while (start < length) {
// 找到k处和2k处
StringBuffer temp = new StringBuffer();
// 与length进行判断,如果大于length了,那就将其置为length
int firstK = (start + k > length) ? length : start + k;
int secondK = (start + (2 * k) > length) ? length : start + (2 * k);
//无论start所处位置,至少会反转一次
temp.append(s.substring(start, firstK));
res.append(temp.reverse());
// 如果firstK到secondK之间有元素,这些元素直接放入res里即可。
if (firstK < secondK) { //此时剩余长度一定大于k。
res.append(s.substring(firstK, secondK));
}
start += (2 * k);
}
return res.toString();
}
}
//解法二(似乎更容易理解点)
//题目的意思其实概括为 每隔2k个反转前k个,尾数不够k个时候全部反转
class Solution {
public String reverseStr(String s, int k) {
char[] ch = s.toCharArray();
for(int i = 0; i < ch.length; i += 2 * k){
int start = i;
//这里是判断尾数够不够k个来取决end指针的位置
int end = Math.min(ch.length - 1, start + k - 1);
//用异或运算反转
while(start < end){
ch[start] ^= ch[end];
ch[end] ^= ch[start];
ch[start] ^= ch[end];
start++;
end--;
}
}
return new String(ch);
}
}
// 解法3
class Solution {
public String reverseStr(String s, int k) {
char[] ch = s.toCharArray();
// 1. 每隔 2k 个字符的前 k 个字符进行反转
for (int i = 0; i< ch.length; i += 2 * k) {
// 2. 剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符
if (i + k <= ch.length) {
reverse(ch, i, i + k -1);
continue;
}
// 3. 剩余字符少于 k 个,则将剩余字符全部反转
reverse(ch, i, ch.length - 1);
}
return new String(ch);
}
// 定义翻转函数
public void reverse(char[] ch, int i, int j) {
for (; i < j; i++, j--) {
char temp = ch[i];
ch[i] = ch[j];
ch[j] = temp;
}
}
}
替换空格
请实现一个函数,把字符串 s 中的每个空格替换成”%20”。
示例 1: 输入:s = “We are happy.”
输出:”We%20are%20happy.”
首先扩充数组到每个空格替换成”%20”之后的大小。
然后从后向前替换空格,也就是双指针法,过程如下:
i指向新长度的末尾,j指向旧长度的末尾。

为什么要从后向前填充,从前向后填充不行么?
从前向后填充就是O(n^2)的算法了,因为每次添加元素都要将添加元素之后的所有元素向后移动。
其实很多数组填充类的问题,都可以先预先给数组扩容带填充后的大小,然后在从后向前进行操作。
这么做有两个好处:
- 不用申请新数组。
- 从后向前填充元素,避免了从前先后填充元素要来的 每次添加元素都要将添加元素之后的所有元素向后移动。
//使用一个新的对象,复制 str,复制的过程对其判断,是空格则替换,否则直接复制,类似于数组复制
public static String replaceSpace(StringBuffer str) {
if (str == null) {
return null;
}
//选用 StringBuilder 单线程使用,比较快,选不选都行
StringBuilder sb = new StringBuilder();
//使用 sb 逐个复制 str ,碰到空格则替换,否则直接复制
for (int i = 0; i < str.length(); i++) {
//str.charAt(i) 为 char 类型,为了比较需要将其转为和 " " 相同的字符串类型
//if (" ".equals(String.valueOf(str.charAt(i)))){
if (s.charAt(i) == ' ') {
sb.append("%20");
} else {
sb.append(str.charAt(i));
}
}
return sb.toString();
}
//方式二:双指针法
public String replaceSpace(String s) {
if(s == null || s.length() == 0){
return s;
}
//扩充空间,空格数量2倍
StringBuilder str = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
if(s.charAt(i) == ' '){
str.append(" ");
}
}
//若是没有空格直接返回
if(str.length() == 0){
return s;
}
//有空格情况 定义两个指针
int left = s.length() - 1;//左指针:指向原始字符串最后一个位置
s += str.toString();
int right = s.length()-1;//右指针:指向扩展字符串的最后一个位置
char[] chars = s.toCharArray();
while(left>=0){
if(chars[left] == ' '){
chars[right--] = '0';
chars[right--] = '2';
chars[right] = '%';
}else{
chars[right] = chars[left];
}
left--;
right--;
}
return new String(chars);
}
翻转字符串里的单词
给定一个字符串,逐个翻转字符串中的每个单词。
示例 1:
输入: “the sky is blue”
输出: “blue is sky the”
示例 2:
输入: “ hello world! “
输出: “world! hello”
解释: 输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
示例 3:
输入: “a good example”
输出: “example good a”
解释: 如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个
使用split库函数,分隔单词,然后定义一个新的string字符串,最后再把单词倒序相加,那么这道题题目就是一道水题了,失去了它的意义。
所以这里我还是提高一下本题的难度:不要使用辅助空间,空间复杂度要求为O(1)。
不能使用辅助空间之后,那么只能在原字符串上下功夫了。
想一下,我们将整个字符串都反转过来,那么单词的顺序指定是倒序了,只不过单词本身也倒序了,那么再把单词反转一下,单词不就正过来了。
所以解题思路如下:
- 移除多余空格
- 将整个字符串反转
- 将每个单词反转
举个例子,源字符串为:”the sky is blue “
- 移除多余空格 : “the sky is blue”
- 字符串反转:”eulb si yks eht”
- 单词反转:”blue is sky the”
class Solution {
/**
* 不使用Java内置方法实现
* <p>
* 1.去除首尾以及中间多余空格
* 2.反转整个字符串
* 3.反转各个单词
*/
public String reverseWords(String s) {
// System.out.println("ReverseWords.reverseWords2() called with: s = [" + s + "]");
// 1.去除首尾以及中间多余空格
StringBuilder sb = removeSpace(s);
// 2.反转整个字符串
reverseString(sb, 0, sb.length() - 1);
// 3.反转各个单词
reverseEachWord(sb);
return sb.toString();
}
private StringBuilder removeSpace(String s) {
// System.out.println("ReverseWords.removeSpace() called with: s = [" + s + "]");
int start = 0;
int end = s.length() - 1;
while (s.charAt(start) == ' ') start++;
while (s.charAt(end) == ' ') end--;
StringBuilder sb = new StringBuilder();
while (start <= end) {
char c = s.charAt(start);
if (c != ' ' || sb.charAt(sb.length() - 1) != ' ') {
sb.append(c);
}
start++;
}
// System.out.println("ReverseWords.removeSpace returned: sb = [" + sb + "]");
return sb;
}
/**
* 反转字符串指定区间[start, end]的字符
*/
public void reverseString(StringBuilder sb, int start, int end) {
// System.out.println("ReverseWords.reverseString() called with: sb = [" + sb + "], start = [" + start + "], end = [" + end + "]");
while (start < end) {
char temp = sb.charAt(start);
sb.setCharAt(start, sb.charAt(end));
sb.setCharAt(end, temp);
start++;
end--;
}
// System.out.println("ReverseWords.reverseString returned: sb = [" + sb + "]");
}
private void reverseEachWord(StringBuilder sb) {
int start = 0;
int end = 1;
int n = sb.length();
while (start < n) {
while (end < n && sb.charAt(end) != ' ') {
end++;
}
reverseString(sb, start, end - 1);
start = end + 1;
end = start + 1;
}
}
}
//解法二:创建新字符数组填充。时间复杂度O(n)
class Solution {
public String reverseWords(String s) {
//源字符数组
char[] initialArr = s.toCharArray();
//新字符数组
char[] newArr = new char[initialArr.length+1];//下面循环添加"单词 ",最终末尾的空格不会返回
int newArrPos = 0;
//i来进行整体对源字符数组从后往前遍历
int i = initialArr.length-1;
while(i>=0){
while(i>=0 && initialArr[i] == ' '){i--;} //跳过空格
//此时i位置是边界或!=空格,先记录当前索引,之后的while用来确定单词的首字母的位置
int right = i;
while(i>=0 && initialArr[i] != ' '){i--;}
//指定区间单词取出(由于i为首字母的前一位,所以这里+1,),取出的每组末尾都带有一个空格
for (int j = i+1; j <= right; j++) {
newArr[newArrPos++] = initialArr[j];
if(j == right){
newArr[newArrPos++] = ' ';//空格
}
}
}
//若是原始字符串没有单词,直接返回空字符串;若是有单词,返回0-末尾空格索引前范围的字符数组(转成String返回)
if(newArrPos == 0){
return "";
}else{
return new String(newArr,0,newArrPos-1);
}
}
}
左旋转字符串
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串”abcdefg”和数字2,该函数将返回左旋转两位得到的结果”cdefgab”。
示例 1:
输入: s = “abcdefg”, k = 2
输出: “cdefgab”
示例 2:
输入: s = “lrloseumgh”, k = 6
输出: “umghlrlose”
限制:
1 <= k < s.length <= 10000
可以通过局部反转+整体反转 达到左旋转的目的。
具体步骤为:
- 反转区间为前n的子串
- 反转区间为n到末尾的子串
- 反转整个字符串
最后就可以得到左旋n的目的,而不用定义新的字符串,完全在本串上操作。
例如 :示例1中 输入:字符串abcdefg,n=2
如图:

最终得到左旋2个单元的字符串:cdefgab
class Solution {
public String reverseLeftWords(String s, int n) {
int len=s.length();
StringBuilder sb=new StringBuilder(s);
reverseString(sb,0,n-1);
reverseString(sb,n,len-1);
return sb.reverse().toString();
}
public void reverseString(StringBuilder sb, int start, int end) {
while (start < end) {
char temp = sb.charAt(start);
sb.setCharAt(start, sb.charAt(end));
sb.setCharAt(end, temp);
start++;
end--;
}
}
}
KMP
KMP主要应用在字符串匹配上。
KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
所以如何记录已经匹配的文本内容,是KMP的重点,也是next数组肩负的重任。
不仅面试的时候可能写不出来,如果面试官问:next数组里的数字表示的是什么,为什么这么表示?
什么是前缀表
前缀表有什么作用呢?
前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
为了清楚的了解前缀表的来历,我们来举一个例子:
要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf。

可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,会发现不匹配,此时就要从头匹配了。
但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
前缀表是如何记录的呢?
首先要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,再重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。
那么什么是前缀表:记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
最长公共前后缀?
文章中字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。
因为前缀表要求的就是相同前后缀的长度。
而最长公共前后缀里面的“公共”,更像是说前缀和后缀公共的长度。这其实并不是前缀表所需要的。
所以字符串a的最长相等前后缀为0。 字符串aa的最长相等前后缀为1。 字符串aaa的最长相等前后缀为2。 等等…..。
为什么一定要用前缀表
这就是前缀表,那为啥就能告诉我们 上次匹配的位置,并跳过去呢?
回顾一下,刚刚匹配的过程在下标5的地方遇到不匹配,模式串是指向f,如图: 
然后就找到了下标2,指向b,继续匹配:如图: 
下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。
所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
如何计算前缀表
怎么计算前缀表。

长度为前1个字符的子串a,最长相同前后缀的长度为0。(注意字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串;后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。)
 长度为前2个字符的子串
长度为前2个字符的子串aa,最长相同前后缀的长度为1。
 长度为前3个字符的子串
长度为前3个字符的子串aab,最长相同前后缀的长度为0。
以此类推: 长度为前4个字符的子串aaba,最长相同前后缀的长度为1。 长度为前5个字符的子串aabaa,最长相同前后缀的长度为2。 长度为前6个字符的子串aabaaf,最长相同前后缀的长度为0。
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图: 
可以看出模式串与前缀表对应位置的数字表示的就是:下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。

找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
为什么要前一个字符的前缀表的数值呢,因为要找前面字符串的最长相同的前缀和后缀。
所以要看前一位的 前缀表的数值。
前一个字符的前缀表的数值是2, 所有把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
前缀表与next数组
很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
其实这并不涉及到KMP的原理,而是具体实现,next数组即可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。
使用next数组来匹配
以下我们以前缀表统一减一之后的next数组来做演示。
有了next数组,就可以根据next数组来 匹配文本串s,和模式串t了。
注意next数组是新前缀表(旧前缀表统一减一了)。
匹配过程动画如下:

时间复杂度分析
其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
暴力的解法显而易见是O(n × m),所以KMP在字符串匹配中极大的提高的搜索的效率。
为了和力扣题目28.实现strStr保持一致,方便大家理解,以下文章统称haystack为文本串, needle为模式串。
都知道使用KMP算法,一定要构造next数组。
构造next数组
我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。
构造next数组其实就是计算模式串s,前缀表的过程。 主要有如下三步:
- 初始化
- 处理前后缀不相同的情况
- 处理前后缀相同的情况
接下来我们详解详解一下。
- 初始化:
定义两个指针i和j,j指向前缀末尾位置,i指向后缀末尾位置。
然后还要对next数组进行初始化赋值.
strStr()
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例 1: 输入: haystack = “hello”, needle = “ll” 输出: 2
示例 2: 输入: haystack = “aaaaa”, needle = “bba” 输出: -1
说明: 当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。 对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符
class Solution {
//前缀表(不减一)Java实现
public int strStr(String haystack, String needle) {
if (needle.length() == 0) return 0;
int[] next = new int[needle.length()];
getNext(next, needle);
int j = 0;
for (int i = 0; i < haystack.length(); i++) {
while (j > 0 && needle.charAt(j) != haystack.charAt(i))
j = next[j - 1];
if (needle.charAt(j) == haystack.charAt(i))
j++;
if (j == needle.length())
return i - needle.length() + 1;
}
return -1;
}
private void getNext(int[] next, String s) {
int j = 0;
next[0] = 0;
for (int i = 1; i < s.length(); i++) {
while (j > 0 && s.charAt(j) != s.charAt(i))
j = next[j - 1];
if (s.charAt(j) == s.charAt(i))
j++;
next[i] = j;
}
}
}
重复的子字符串
给定一个非空的字符串,判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母,并且长度不超过10000。
示例 1:
输入: “abab”
输出: True
解释: 可由子字符串 “ab” 重复两次构成。
示例 2:
输入: “aba”
输出: False
示例 3:
输入: “abcabcabcabc”
输出: True
解释: 可由子字符串 “abc” 重复四次构成。 (或者子字符串 “abcabc” 重复两次构成。)
在由重复子串组成的字符串中,最长相等前后缀不包含的子串就是最小重复子串,这里那字符串s:abababab 来举例,ab就是最小重复单位,如图所示:
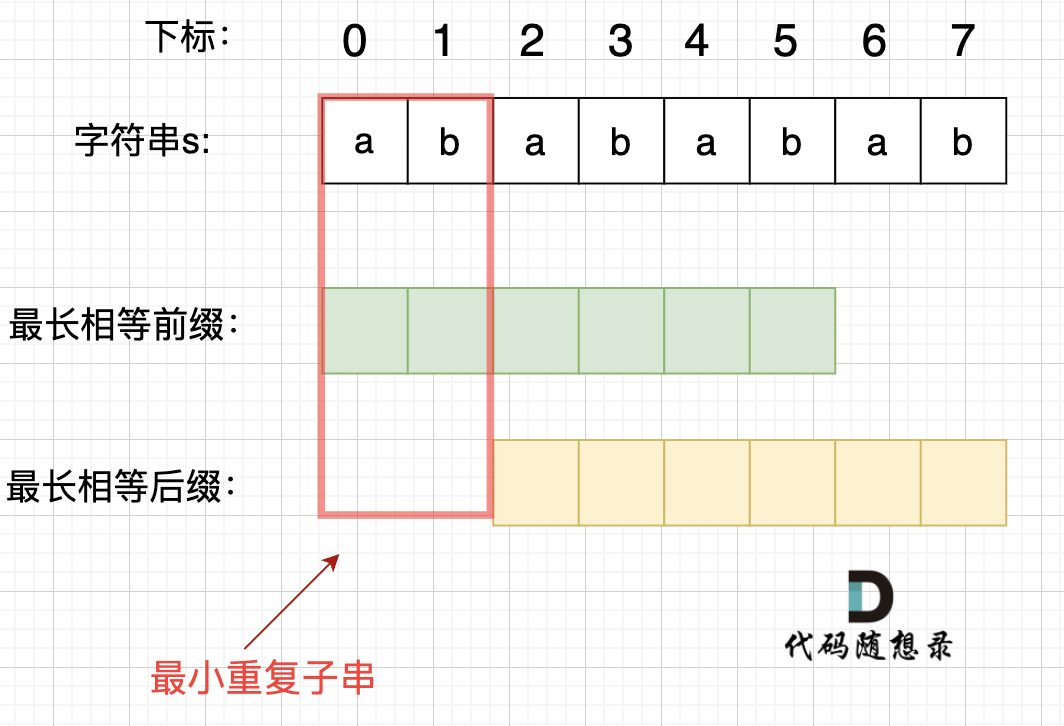
如何找到最小重复子串
这里有同学就问了,为啥一定是开头的ab呢。 其实最关键还是要理解 最长相等前后缀,如图:
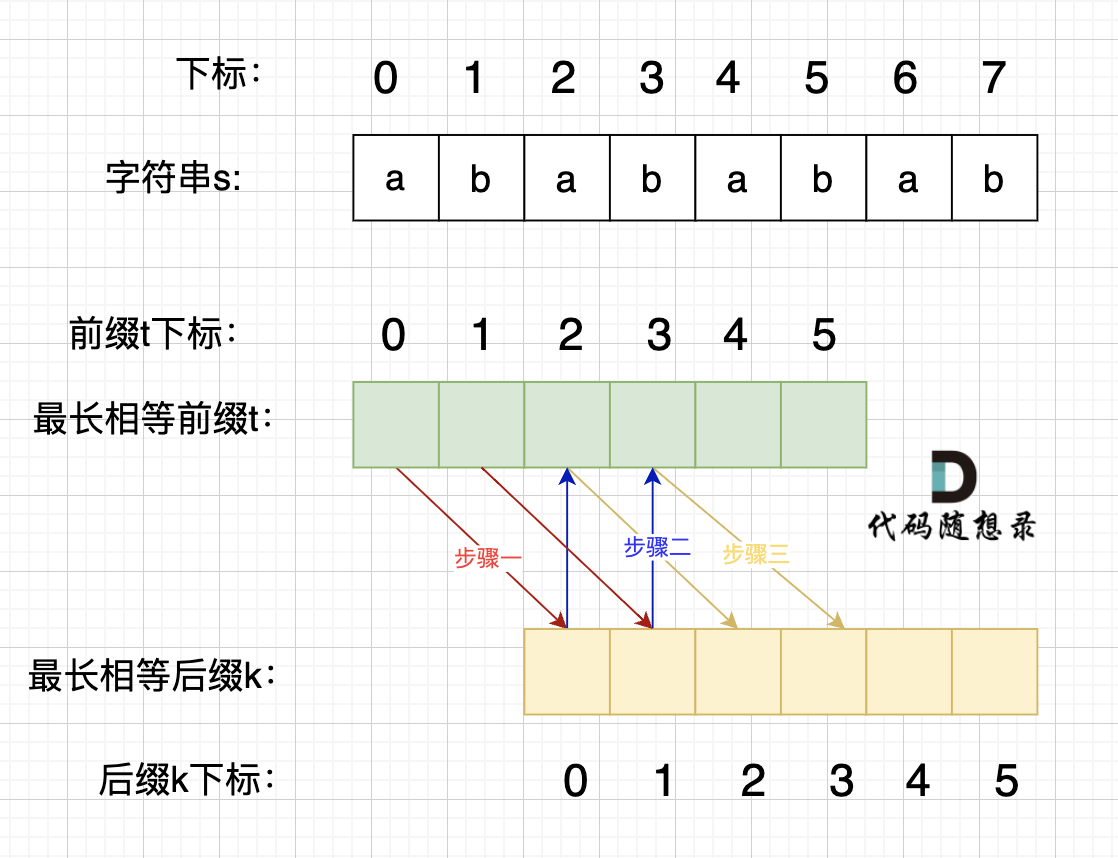
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,所以 s[0] 一定和 s[2]相同,s[1] 一定和 s[3]相同,即:,s[0]s[1]与s[2]s[3]相同 。
步骤二: 因为在同一个字符串位置,所以 t[2] 与 k[0]相同,t[3] 与 k[1]相同。
步骤三: 因为 这是相等的前缀和后缀,t[2] 与 k[2]相同 ,t[3]与k[3] 相同,所以,s[2]一定和s[4]相同,s[3]一定和s[5]相同,即:s[2]s[3] 与 s[4]s[5]相同。
步骤四:循环往复。
所以字符串s,s[0]s[1]与s[2]s[3]相同, s[2]s[3] 与 s[4]s[5]相同,s[4]s[5] 与 s[6]s[7] 相同。
正是因为 最长相等前后缀的规则,当一个字符串由重复子串组成的,最长相等前后缀不包含的子串就是最小重复子串。
简单推理
这里在给出一个数推导,就容易理解很多。
假设字符串s使用多个重复子串构成(这个子串是最小重复单位),重复出现的子字符串长度是x,所以s是由n * x组成。
因为字符串s的最长相同前后缀的的长度一定是不包含s本身,所以 最长相同前后缀长度必然是m * x,而且 n - m = 1,(这里如果不懂,看上面的推理)
所以如果 nx % (n - m)x = 0,就可以判定有重复出现的子字符串。
class Solution {
public boolean repeatedSubstringPattern(String s) {
if(s.length()==0){
return false;
}
int[] next=new int[s.length()];
getNext(next,s);
int len=s.length();
if(next[s.length()-1]!=0 && len%(len-next[s.length()-1])==0){
return true;
}
return false;
}
void getNext(int[] next,String s){
int j=0;
next[0]=0;
for(int i=1;i<s.length();i++){
while(j>0 && s.charAt(i)!=s.charAt(j)){
j=next[j-1];
}
if(s.charAt(i)==s.charAt(j)){
j++;
}
next[i]=j;
}
}
}
总结:
使用双指针法实现了反转字符串的操作,双指针法在数组,链表和字符串中很常用。
接着在字符串:替换空格 (opens new window),同样还是使用双指针法在时间复杂度O(n)的情况下完成替换空格。
其实很多数组填充类的问题,都可以先预先给数组扩容带填充后的大小,然后在从后向前进行操作。
反转字符串II (opens new window)中,一些同学可能为了处理逻辑:每隔2k个字符的前k的字符,写了一堆逻辑代码或者再搞一个计数器,来统计2k,再统计前k个字符。
其实当需要固定规律一段一段去处理字符串的时候,要想想在在for循环的表达式上做做文章。
只要让 i += (2 * k),i 每次移动 2 * k 就可以了,然后判断是否需要有反转的区间。
因为要找的也就是每2 * k 区间的起点,这样写程序会高效很多。
在翻转字符串里的单词 (opens new window)中,通过 先整体反转再局部反转,实现了反转字符串里的单词。
KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
前缀:指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀:指不包含第一个字符的所有以最后一个字符结尾的连续子串。
然后针对前缀表到底要不要减一,这其实是不同KMP实现的方式